Nhiệm vụ. Kiểm tra đô thị liên thông Một đồ thị được gọi là liên thông nếu tồn tại

Giải Chuyên đề Tin 12 Bài 3.4: Duyệt đồ thị theo chiều sâu - Chân trời sáng tạo

Vận dụng trang 71 Chuyên đề Tin học 12: Nhiệm vụ. Kiểm tra đô thị liên thông

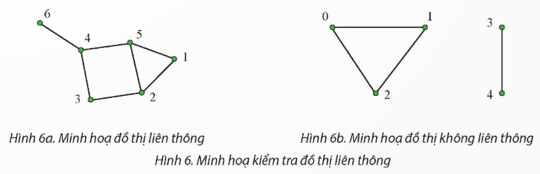
Một đồ thị được gọi là liên thông nếu tồn tại ít nhất một đường đi giữa hai đỉnh bất kì của nó. Chẳng hạn, đồ thị ở Hình 6a là liên thông còn đô thị ở Hình 6b là không liên thông (không có đường đi từ đỉnh 0 tới đỉnh 3).

Yêu cầu: Áp dụng thuật toán duyệt đồ thị theo chiều sâu. Thực hiện xây dựng thuật toán kiểm tra xem đồ thị G = (V, E) cho trước có liên thông hay không.

Lời giải:

Áp dụng thuật toán duyệt đồ thị theo chiều sâu. Thực hiện xây dựng thuật toán kiểm tra xem đồ thị G = (V, E) cho trước có liên thông hay không.

def dft(graph, u): stack initStack()

#Khởi tạo stack rỗng

visited [vertices.index(u)] = True #Đánh dấu đỉnh u đã duyệt

print(u, end = " ")

push(stack, u)

#In đỉnh u

#Thêm đỉnh u vào stack

while not isEmptyStack(stack): #Lặp khi stack khác rỗng

p = top(stack)

found = False

for v in graph[p]:

#Xem đỉnh p ở đỉnh stack

#Chưa tìm thấy

#Lặp để lấy các đỉnh kề v của đỉnh p

if not visited[vertices.index(v)]: #Nếu đỉnh v chưa duyệt

found = True

break

if not found:

p = pop(stack)

else:

#Tìm thấy

#Không tìm thấy đỉnh v

#Lấy đỉnh p ra khỏi stack

#Tìm thấy đỉnh v chưa duyệt

visited[vertices.index(v)] = True #Đánh dấu đỉnh v đã duyệt

print(v, end = "")

push(stack, v)

#In đỉnh v

#Thêm đỉnh v vào stack

#Hàm duyệt graph dạng danh sách kế theo chiều sâu

def dfs(graph):

global visited

visited [False]

*

len(graph)

for u in graph:

if not visited [vertices.index(u)]:

dft(graph, u)

#Đánh dấu các đỉnh chưa duyệt

#Xét đỉnh u chưa duyệt

#Duyệt đô thị theo chiều sâu từ u

graph, vertices = createAdjListGraph('dothi.txt') #Tạo đô thị từ tập dfs(graph)

#In kết quả duyệt theo chiều sâu

Lời giải bài tập Chuyên đề Tin 12 Bài 3.4: Duyệt đồ thị theo chiều sâu hay, chi tiết khác:

• Khởi động trang 64 Chuyên đề Tin học 12: Cho đồ thị G1 như ở Hình 1. Hãy tìm đường đi ngắn nhất từ đỉnh H đến đỉnh D ....

• Câu hỏi trang 68 Chuyên đề Tin học 12: Em hãy minh hoạ duyệt theo chiều sâu của đồ thị G2 ở Hình 2 ....

• Câu hỏi trang 69 Chuyên đề Tin học 12: Hãy liệt kê thứ tự duyệt các đỉnh với thuật toán duyệt đồ thị theo chiều sâu xuất phát từ đỉnh A ....

• Luyện tập 1 trang 70 Chuyên đề Tin học 12: Dùng thuật toán duyệt đồ thị theo chiều sâu xuất phát từ đỉnh 1 ....

• Luyện tập 2 trang 70 Chuyên đề Tin học 12: Cho đồ thị G5 (Hình 5). Chỉ ra đường đi từ đỉnh F đến đỉnh J bằng thuật toán duyệt đồ thị ....

• Thực hành trang 70 Chuyên đề Tin học 12: Nhiệm vu: Duyệt đồ thị theo chiều sâu ....

Xem thêm lời giải bài tập Chuyên đề học tập Tin học 12 Chân trời sáng tạo hay, chi tiết khác:

• Chuyên đề Tin 12 Bài 2.4: Thực hành cây tìm kiếm nhị phân

• Chuyên đề Tin 12 Bài 3.1: Các khái niệm cơ bản của đồ thị

• Chuyên đề Tin 12 Bài 3.2: Biểu diễn đồ thị

• Chuyên đề Tin 12 Bài 3.3: Duyệt đồ thị theo chiều rộng

• Chuyên đề Tin 12 Bài 3.5: Thực hành kĩ thuật duyệt đồ thị

Xem thêm các tài liệu học tốt lớp 12 hay khác:

• Giải Chuyên đề Tin học 12 Kết nối tri thức
• Giải Chuyên đề Tin học 12 Chân trời sáng tạo
• Giải Chuyên đề Tin học 12 Cánh diều
• Giải lớp 12 Kết nối tri thức (các môn học)
• Giải lớp 12 Chân trời sáng tạo (các môn học)
• Giải lớp 12 Cánh diều (các môn học)

---