Các bài toán liên quan đến công thức xác suất toàn phần lớp 12 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Các bài toán liên quan đến công thức xác suất toàn phần lớp 12 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Các bài toán liên quan đến công thức xác suất toàn phần.

Các bài toán liên quan đến công thức xác suất toàn phần lớp 12 (cách giải + bài tập)

1. Phương pháp giải

Cho hai biến cố A và B với 0 < P(B) < 1. Khi đó:

$P\left(A\right)=P\left(B\right).P\left(A|B\right)+P\left(\overline{B}\right).P\left(A|\overline{B}\right)$.

Chú ý: Công thức xác suất toàn phần cũng đúng với biến cố B bất kì.

2. Ví dụ minh họa

Ví dụ 1. Hộp thứ nhất có 3 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 7 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ hai. Tính xác suất để hai viên bi lấy ra từ hộp thứ hai là bi đỏ.

Hướng dẫn giải:

Gọi A là biến cố: “Lấy được một viên bi màu xanh ở hộp thứ nhất”;

B là biến cố: “Lấy được hai viên bi màu đỏ ở hộp thứ hai”.

Khi đó $P\left(A\right)=\frac{1}{3};P\left(B|A\right)=\frac{C_7^2}{C_{11}^2}=\frac{21}{55}$.

Suy ra $P\left(\overline{A}\right)=1-P\left(A\right)=\frac{2}{3};P\left(B|\overline{A}\right)=\frac{C_8^2}{C_{11}^2}=\frac{28}{55}$.

Áp dụng công thức xác suất toàn phần ta có:

$P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)=\frac{1}{3}.\frac{21}{55}+\frac{2}{3}.\frac{28}{55}=\frac{7}{15}$.

Ví dụ 2. Tại nhà máy X sản xuất linh kiện điện tử tỉ lệ sản phẩm đạt tiêu chuẩn là 80%. Trước khi xuất xưởng ra thị trường, các linh kiện điện tử đều phải qua khâu kiểm tra chất lượng để đóng dấu OTK. Vì sự kiểm tra không tuyệt đối hoàn hảo nên nếu một linh kiện điện tử đạt tiêu chuẩn thì nó có xác suất 0,99 được đóng dấu OTK, nếu một linh kiện điện tử không đạt tiêu chuẩn thì nó có xác suất 0,95 không được đóng dấu OTK. Chọn ngẫu nhiên một linh kiện điện tử của nhà máy X trên thị trường. Tính xác suất để linh kiện điện tử đó được đóng dấu OTK.

Hướng dẫn giải:

Gọi A là biến cố: “Linh kiện điện tử đạt tiêu chuẩn”; B là biến cố: “Linh kiện điện tử được đóng dấu OTK”. Ta cần tính P(B).

Theo đề ta có: P(A) = 0,8; P(B|A) = 0,99; $P\left(\overline{B}|\overline{A}\right)=0,95$.

Suy ra $P\left(\overline{A}\right)=1-0,8=0,2;P\left(B|\overline{A}\right)=1-0,95=0,05$.

Do đó $P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)=0,8.0,99+0,2.0,05=0,802$.

3. Bài tập tự luyện

Bài 1. Cho hai biến cố A, B với P(B) = 0,6; P(A|B) = 0,7 và $P\left(A|\overline{B}\right)=0,4$. Khi đó P(A) bằng

A. 0,7;

B. 0,4;

C. 0,58;

D. 0,52.

Hướng dẫn giải:

Đáp án đúng là: C

Ta có $P\left(\overline{B}\right)=1-P\left(B\right)=1-0,6=0,4$.

Theo công thức xác suất toàn phần, ta có:

$P\left(A\right)=P\left(B\right).P\left(A|B\right)+P\left(\overline{B}\right).P\left(A|\overline{B}\right)=0,6.0,7+0,4.0,4=0,58$.

Bài 2. Cho hai biến cố A và B biết P(A|B) = 0,08; $P\left(\overline{A}|\overline{B}\right)=0,63$; P(B) = 0,03. Khi đó xác suất xảy ra biến cố A là bao nhiêu?

A. 0,112;

B. 0,5231;

C. 0,3613;

D. 0,063.

Hướng dẫn giải:

Đáp án đúng là: C

Ta có P(B) = 0,03$\Rightarrow P\left(\overline{B}\right)=1-0,03=0,97$.

$P\left(\overline{A}|\overline{B}\right)=0,63\Rightarrow P\left(A|\overline{B}\right)=1-0,63=0,37$.

Theo công thức xác suất toàn phần:

$P\left(A\right)=P\left(B\right).P\left(A|B\right)+P\left(\overline{B}\right).P\left(A|\overline{B}\right)$ = 0,03.0,08 + 0,97.0,37 = 0,3613.

Bài 3. Cho A, B là hai biến cố. Biết P(B) = 0,2. Nếu B không xảy ra thì tỉ lệ A xảy ra là 2%. Nếu B xảy ra thì tỉ lệ A xảy ra 4%. Xác suất của biến cố A là bao nhiêu?

A. 0,018;

B. 0,036;

C. 0,028;

D. 0,024.

Hướng dẫn giải:

Đáp án đúng là: D

Ta có P(B) = 0,2 $\Rightarrow P\left(\overline{B}\right)=0,8$.

Vì B xảy ra thì tỉ lệ A xảy ra 4% nên P(A|B) = 0,04.

Tương tự ta có $P\left(A|\overline{B}\right)=0,02$.

Theo công thức xác suất toàn phần ta có:

$P\left(A\right)=P\left(B\right).P\left(A|B\right)+P\left(\overline{B}\right).P\left(A|\overline{B}\right)$ = 0,2.0,04 + 0,8.0,02 = 0,024.

Bài 4. Có hai hộp đựng các viên bi. Hộp thứ nhất đựng 5 bi đỏ và 3 bi vàng, hộp thứ hai đựng 4 bi đỏ và 2 bi vàng. Lấy ngẫu nhiên một bi từ hộp thứ nhất bỏ sang hộp thứ hai, sau đó lấy ngẫu nhiên một bi từ hộp thứ hai. Xác suất để bi lấy ra từ hộp thứ hai là bi đỏ thuộc khoảng nào sau đây?

A. (0,65; 0,67);

B. (0,57; 0,59);

C. (0,61; 0,63);

D. (0,63; 0,65).

Hướng dẫn giải:

Đáp án đúng là: A

Gọi A là biến cố: “Lấy bi đỏ từ hộp thứ nhất bỏ sang hộp thứ hai”,

B là biến cố: “Lấy được bi đỏ từ hộp thứ hai”.

Ta có $P\left(A\right)=\frac{5}{8};P\left(B|A\right)=\frac{5}{7}$; $P\left(\overline{A}\right)=\frac{3}{8};P\left(B|\overline{A}\right)=\frac{4}{7}$.

Vậy $P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)=\frac{5}{8}.\frac{5}{7}+\frac{3}{8}.\frac{4}{7}=\frac{37}{56}\approx 0,661$.

Bài 5. Một lớp học có số lượng học sinh nam chiếm 65%. Tỉ lệ học sinh nam học khá môn Tiếng Anh là 75%, tỉ lệ học sinh nữ học khá môn Tiếng Anh là 82%. Nếu ta gặp ngẫu nhiên một bạn học sinh trong lớp thì xác suất để bạn học sinh này học khá môn Tiếng Anh thuộc khoảng nào sau đây.

A. (0,7; 0,75);

B. (0,65; 0,7);

C. (0,75; 0,8);

D. (0,8; 0,85).

Hướng dẫn giải:

Đáp án đúng là: C

Gọi biến cố A: “Gặp một học sinh nam”, biến cố B: “Gặp một học sinh học khá môn Tiếng Anh”.

Ta có P(A) = 65% = 0,65; P(B|A) = 75% = 0,75;

$P\left(\overline{A}\right)=35\%=0,35;P\left(B|\overline{A}\right)=82\%=0,82$.

Khi đó $P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)=0,65.0,75+0,35.0,82=0,7745$.

Bài 6. Hai máy tự động sản xuất cùng một loại chi tiết, trong đó máy I sản xuất 35%, máy II sản xuất 65% tổng sản lượng. Tỉ lệ phế phẩm của các máy lần lượt là 0,3% và 0,7%. Chọn ngẫu nhiên 1 sản phẩm từ kho. Tính xác suất để chọn được phế phẩm.

A. 0,0056;

B. 0,0065;

C. 0,065;

D. 0,056.

Hướng dẫn giải:

Đáp án đúng là: A

Gọi A là biến cố: “Sản phẩm được chọn do máy I sản xuất”;

B là biến cố: “Sản phẩm được chọn là phế phẩm”.

Theo đề ta có P(A) = 0,35; ; P(B|A) = 0,003; .

Suy ra $P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)=0,35.0,003+0,65.0,007=0,0056$.

Bài 7. Có 2 xạ thủ loại I và 8 xạ thủ loại II, xác suất bắn trúng đích của các loại xạ thủ loại I là 0,9 và loại II là 0,7. Chọn ngẫu nhiên ra một xạ thủ và xạ thủ đó bắn một viên đạn. Tìm xác suất để viên đạn đó trúng đích.

A. 0,74;

B. 0,86;

C. 0,56;

D. 0,68.

Hướng dẫn giải:

Đáp án đúng là: A

Gọi A là biến cố: “Viên đạn trúng đích”, B là biến cố: “Chọn xạ thủ loại I bắn”.

Theo đề ta có $P\left(\overline{A}\right)=0,65$; P(A|B) = 0,9; $P\left(B|\overline{A}\right)=0,007$.

Do đó ta có = 0,2.0,9 + 0,8.0,7 = 0,74.

Bài 8. Một hộp bút bi Thiên Long có 15 chiếc bút trong đó có 9 chiếc bút mới. Người ta lấy ngẫu nhiên 1 chiếc bút để sử dụng sau đó trả lại vào hộp. Lần thứ hai lấy ngẫu nhiên 2 chiếc bút, tính xác suất cả hai chiếc bút lấy ra đều là chiếc mới.

A. $\frac{52}{175}$;

B. $\frac{52}{177}$;

C. $\frac{53}{175}$;

D. $\frac{25}{175}$.

Hướng dẫn giải:

Đáp án đúng là: A

Gọi A là biến cố: “Hai chiếc bút lấy ra đều là chiếc mới”;

B là biến cố: “Lấy ra một chiếc bút cũ”.

Theo đề ta có $P\left(B\right)=\frac{C_6^1}{C_{15}^1}=\frac{2}{5}\Rightarrow P\left(\overline{B}\right)=\frac{3}{5}$.

$P\left(A|B\right)=\frac{C_9^2}{C_{15}^2}=\frac{12}{35};P\left(A|\overline{B}\right)=\frac{C_8^2}{C_{15}^2}=\frac{4}{15}$.

Do đó $P\left(A\right)=P\left(B\right).P\left(A|B\right)+P\left(\overline{B}\right).P\left(A|\overline{B}\right)=\frac{12}{35}.\frac{2}{5}+\frac{4}{15}.\frac{3}{5}=\frac{52}{175}$.

Bài 9. Giả sử tỉ lệ người dân của tỉnh Khánh Hòa nghiện thuốc lá là 20%, tỉ lệ người bị bệnh phổi trong số người nghiện thuốc là là 70%, trong số người không nghiện thuốc là là 15%. Hỏi khi ta gặp ngẫu nhiên một người dân của tỉnh Khánh Hòa thì khả năng mà người đó bị bệnh phổi là

A. 15%;

B. 29%;

C. 31%;

D. 26%.

Hướng dẫn giải:

Đáp án đúng là: D

Gọi A là biến cố: “Người đó nghiện thuốc lá”; B là biến cố: “Người đó bị bệnh phổi”.

Theo đề ta có P(A) = 0,2; P(B|A) = 0,7; $P\left(\overline{A}\right)=0,8;P\left(B|\overline{A}\right)=0,15$.

Do đó $P\left(B\right)=P\left(A\right).P\left(B|A\right)+P\left(\overline{A}\right).P\left(B|\overline{A}\right)=0,2.0,7+0,8.0,15=0,26$.

Vậy, tỉ lệ người đó mắc bệnh phổi của tỉnh Khánh Hòa là 26%.

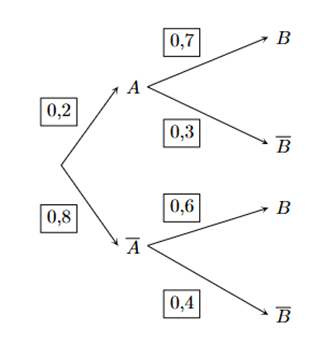
Bài 10. Cho sơ đồ hình cây như hình bên.

Xác suất của biến cố B là

A. 0,42;

B. 0,62;

C. 0,28;

D. 0,48.

Hướng dẫn giải:

Đáp án đúng là: B

Xác suất của biến cố B là P(B) = 0,2.0,7 + 0,8.0,6 = 0,62.

Xem thêm các dạng bài tập Toán 12 hay, chi tiết khác:

• Viết phương trình mặt cầu đi qua 4 điểm không đồng phẳng
• Viết phương trình mặt cầu có tâm và tiếp xúc với một mặt phẳng
• Vận dụng phương trình mặt cầu vào giải quyết bài toán liên quan đến thực tiễn
• Tính xác suất có điều kiện
• Tính xác suất có điều kiện bằng cách sử dụng sơ đồ hình cây
• Các bài toán liên quan đến công thức Bayes

---