11 Chuyên đề Toán thực tế lớp 12 chương trình mới (có lời giải)
Tài liệu 11 Chuyên đề Toán thực tế lớp 12 có lời giải chương trình mới dùng chung cho ba sách Kết nối tri thức, Chân trời sáng tạo, Cánh diều được biên soạn theo từng chuyên đề giúp Giáo viên có thêm tài liệu giảng dạy các dạng toán thực tế lớp 12. Mời các bạn đón đọc:
11 Chuyên đề Toán thực tế lớp 12 chương trình mới (có lời giải)
Chỉ từ 300k mua trọn bộ Chuyên đề, các dạng Toán thực tế lớp 12 chương trình mới bản word trình bày đẹp mắt, chỉnh sửa dễ dàng:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
Bài toán thực tế lớp 12 Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài toán thực tế lớp 12 Ứng dụng đạo hàm để giải quyết bài toán liên quan thực tiễn
Bài toán thực tế lớp 12 Vectơ và tọa độ của vectơ trong không gian
Bài toán thực tế lớp 12 Ứng dụng nguyên hàm giải bài toán thực tiễn
Bài toán thực tế lớp 12 Ứng dụng tích phân giải bài toán thực tiễn liên quan đến Vật lí
Bài toán thực tế lớp 12 Tính đơn điệu và cực trị của hàm số
A. LÝ THUYẾT CẦN NHỚ
1. Tính đơn điệu của hàm số
Định nghĩa: Cho hàm số xác định trên K với K là một khoảng, một đoạn hoặc một nửa khoảng
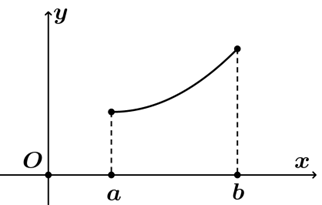
Hình 1. Hàm số đồng biến trên (a; b)
• Hàm số được gọi là đồng biến trên K nếu .
• Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải (Hình 1)
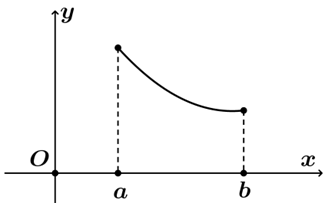
Hình 2. Hàm số nghịch biến trên (a; b)
• Hàm số được gọi là nghịch biến trên K nếu .
• Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải (Hình 2)
• Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.
• Khi xét tính đơn điệu mà không chỉ rõ tập K thì ta hiểu là xét trên tập xác định của hàm số đó.
Liên hệ giữa đạo hàm và tính đơn điệu:
Định lí 1: Cho hàm số có đạo hàm trên khoảng K.
• Nếu và xảy ra tại một số hữu hạn điểm trên K thì hàm số đồng biến trên khoảng K.
• Nếu và xảy ra tại một số hữu hạn điểm trên K thì hàm số nghịch biến trên khoảng K.
Chú ý: Nếu hàm số đồng biến trên tập K hoặc nghịch biến trên tập K thì hàm số còn được gọi là đơn điệu trên tập .
Định lí 2: Cho hàm số có đạo hàm trên tập , trong đó K là một khoảng, đoạn hoặc nửa khoảng. Nếu (hoặc ) với mọi x thuộc K và chỉ tại một số hữu hạn điểm của K thì hàm số đồng biến (hoặc nghịch biến) trên K.
2. Cực trị của hàm số
Định nghĩa: Cho hàm số liên tục trên khoảng (a; b) và điểm .
• Nếu tồn tại số h > 0 sao cho với mọi và thì ta nói hàm số đạt cực đại tại .
• Nếu tồn tại số h > 0 sao cho với mọi và thì ta nói hàm số đạt cực tiểu tại .
Ghi chú:
• Nếu hàm số đạt cực đại tại thì được gọi là điểm cực đại của hàm số, được gọi là giá trị cực đại của hàm số, kí hiệu hay , còn điểm được gọi là điểm cực đại của đồ thị hàm số.
• Nếu hàm số đạt cực tiểu tại thì được gọi là điểm cực tiểu của hàm số, được gọi là giá trị cực tiểu của hàm số, kí hiệu hay , còn điểm được gọi là điểm cực tiểu của đồ thị hàm số.
• Các điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (còn gọi là cực đại) và giá trị cực tiểu (còn gọi là cực tiểu) được gọi chung là giá trị cực trị (hay cực trị) của hàm số.
• Nếu hàm số có đạo hàm trên khoảng (a; b) và có điểm cực trị là thì
Định lí: Giả sử hàm số liên tục trên khoảng và có đạo hàm trên K hoặc trên , với h > 0.
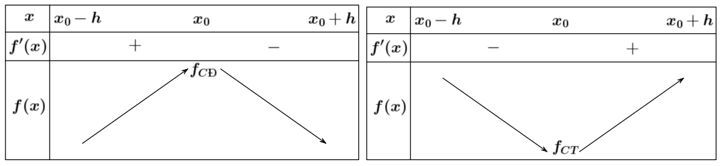
• Nếu trên khoảng và trên khoảng thì là một điểm cực đại của hàm số .
• Nếu trên khoảng và trên khoảng thì là một điểm cực tiểu của hàm số .
Nhận xét: Định lí trên có thể hiểu một cách đơn giản như sau: Điều kiện đủ để hàm số đạt cực trị tại một điểm là đạo hàm đổi dấu khi x qua với .
Nếu hàm số đạt cực trị tại thì hoặc không tồn tại.
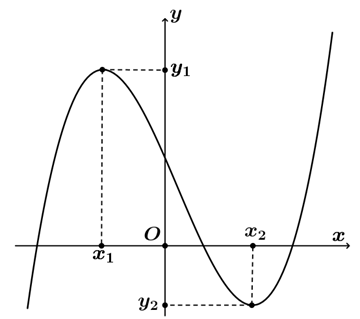
Các tên gọi từ đồ thị hàm số:
• là điểm cực đại của đồ thị hàm số trong đó: là điểm cực đại của hàm số; là giá trị cực đại của hàm số.
• là điểm cực tiểu của đồ thị hàm số trong đó: là điểm cực tiểu của hàm số; là giá trị cực tiểu của hàm số.
B. BÀI TẬP
Bài 1. Một vật được phóng thẳng đứng lên trên từ độ cao 2 m với vận tốc ban đầu là 24,5 m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức . Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Lời giải
Xét hàm số: .
Tập xác định của hàm số là .
Ta có:
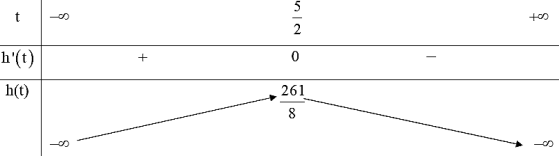
BBT
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại ,
Vậy thời điểm vật đạt độ cao lớn nhất là giây.
Bài 2. Thể tích V (đơn vị: centimét khối) của 1kg nước tại nhiệt độ T () được tính bởi công thức
Hỏi thể tích , , giảm trong khoảng nhiệt độ nào?
Lời giải
Xét hàm số với
Ta có
Khi
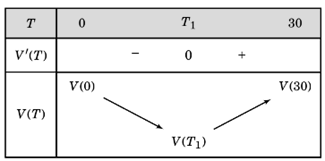
Bảng biến thiên của hàm số V (T) như sau:
Từ bảng biến thiên suy ra, thể tích V (T), , giảm trong khoảng nhiệt độ đến nhiệt độ .
Bài 3. Xét một chất điểm chuyển động dọc theo trục Ox. Toạ độ của chất điểm tại thời điểm t được xác định bởi hàm số với . Khi đó là vận tốc của chất điểm tại thời điểm t, kí hiệu là gia tốc chuyển động của chất điểm tại thời điểm t, kí hiệu
Xét tính đúng sai của các khẳng định sau:
a) Phương trình hàm vận tốc là
b) Phương trình hàm gia tốc là
c) Vận tốc của chất điểm tăng khi
d) Vận tốc của chất điểm giảm khi
Bài 4. Giả sử doanh số (tính bẳng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số , trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Bài 5. Độ giảm huyết áp của một bệnh nhân được xác đinh bởi hàm , trong đó x là số miligam thuốc được tiêm cho bệnh nhân . Để bệnh nhân đó có huyết áp giảm nhiều nhất thì liều lượng thuốc cần tiêm vào là bao nhiêu.
Bài 6. Xét một chất điểm chuyển động dọc theo trục Ox. Toạ độ của chất điểm tại thời điểm t
được xác định bởi hàm số với . Khi đó là vận tốc của chất điểm tại thời điểm t, kí hiệu là gia tốc chuyển động của chất điểm tại thời điểm t, kí hiệu .
a) Tìm các hàm và .
b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
Bài 7. Một chuyển động xác định bởi phương trình với , trong đó t tính bằng giây và s tính bằng mét. Biết bắt đầu từ giây thứ t0 thì vận tốc của vật bắt đầu tăng. Tính t0.
................................
................................
................................
Xem thêm đề thi lớp 12 các môn học có đáp án hay khác:
Đề ôn thi Tốt nghiệp (các môn học), ĐGNL, ĐGTD các trường có đáp án hay khác:
Tài liệu giáo án lớp 12 các môn học chuẩn khác:
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

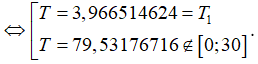



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

