Chu kì con lắc đơn là gì? Công thức tính chu kì con lắc đơn (chi tiết nhất)

Bài viết Chu kì con lắc đơn là gì? Công thức tính chu kì con lắc đơn với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Chu kì con lắc đơn là gì? Công thức tính chu kì con lắc đơn.

Chu kì con lắc đơn là gì? Công thức tính chu kì con lắc đơn (chi tiết nhất)

1. Khái niệm về con lắc đơn

Con lắc đơn là một hệ bao gồm một vật nhỏ có khối lượng m, được treo ở đầu một sợi dây không giãn. Khối lượng của nó nhỏ không đáng kể với chiều dài là l, đầu trên của sợi dây được treo vào một điểm cố định.

2. Con lắc đơn cân bằng ở vị trí nào?

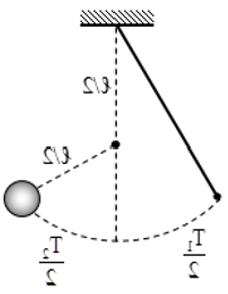
Vị trí cân bằng của con lắc chính là vị trí dây treo có phương thẳng đứng. Hoặc khi kéo nhẹ quả cầu cho dây treo lệch ra khỏi vị trí cân bằng một góc rồi thả tay ra, ta sẽ thấy sự dao động của con lắc quanh vị trí cân bằng trong mặt phẳng đứng đi qua điểm treo và vị trí ban đầu của vật. Từ đó hãy xem dao động của con lắc có phải là dao động điều hòa hay không.

3. Tổng hợp các công thức về con lắc đơn

3.1. Phương trình dao động

Ta có phương trình dao động của con lắc đơn có dạng như sau:

$\left[\begin{array}{l}s=S\cos \left(\omega t+\phi \right)\\ \alpha ={\alpha }_0\cos \left(\omega t+\phi \right)\end{array}\right.$ Với $s=1.\alpha$

Giải thích các đơn vị phương trình:

s: cung dao động(cm,m,…)

S: biên độ cung (cm,m,…)

$\alpha$ : li độ góc(rad)

${\alpha }_0$ : biên độ góc(rad)

$\omega =\sqrt{\frac{g}{1}}(rad/s)$ (g là gia tốc trọng trường và chiều dài của dây treo)

3.2. Phương trình vận tốc gia tốc

● Vận tốc của con lắc khi dao động: $v=s’=\omega .S_o.sin\left(\omega .t+\phi +\frac{\pi }{2}\right)$

$\Rightarrow v_{max}=\omega .$ So khi vật qua vị trí cân bằng

Vận tốc v và li độ s (hoặc li độ góc alpha) vuông pha nhau nên ta sẽ có công thức:

${\left(\frac{v}{v_{max}}\right)}^2+{\left(\frac{s}{S_0}\right)}^2=1$ hoặc ${\left(\frac{v}{v_{max}}\right)}^2+{\left(\frac{\alpha }{{\alpha }_o}\right)}^2=1$

● Phương trình gia tốc

Trong quá trình con lắc chuyển động, nó chịu 2 gia tốc là: gia tốc hướng tâm và gia tốc tiếp tuyến. Phương trình gia tốc tiếp tuyến là: $att=v^{\text{'}}=-{\omega }^2.S_o.cos(\omega .t+\pi )=-{\omega }^2.s$

Gia tốc att và vận tốc v vuông góc với nhau nên ta có hệ thức: ${\left(\frac{a}{at{t}_{max}}\right)}^2+{\left(\frac{v}{v_{max}}\right)}^2=1$

● Phương trình gia tốc hướng tâm: $aht=\frac{v²}{l}$

Gia tốc hướng tâm và gia tốc tiếp tuyến vuông góc với nhau

Vậy ta có gia tốc tổng hợp là: $ath=\sqrt{\left(ah{t}^2+at{t}^2\right)}$

3.3. Chu kì và tần số

Công thức tính chu kỳ: $T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{1}{g}}\left(s\right)$

Công thức tính tần số: $f=\frac{\omega }{2\pi }=\sqrt{\frac{g}{l}}\left(Hz\right)$

Lưu ý:

● Con lắc đơn có chiều dài bằng $l_1$ thì sẽ dao động với tần số là $f_1$

● Con lắc đơn có chiều dài là $l_2$ thì sẽ dao động với tần số là $f_2$

● Con lắc đơn có chiều dài $l=\left(l_1\pm l_2\right)$ thì sẽ dao động với chu kỳ và tần số là: $T=\sqrt{\left({T_1}^2\pm {T_2}^2\right)}{f}^{-2}=\left(f_1^{-2}\pm f_2^{-2}\right)$

3.4. Vận tốc và lực căng dây

Công thức tính vận tốc: $V=\sqrt{2g\left(\text{cos}\alpha \text{-cos}{\alpha }_0\right)}\Rightarrow v_{\max }=\sqrt{2gl\left(1-\cos {\alpha }_0\right)}$

Công thức tính lực căng dây T: $T=mg\left(3\cos \alpha -2\cos {\alpha }_0\right)$

$\Rightarrow T_{\max }=mg\left(3\cos \alpha -2\cos {\alpha }_0\right)$ (vật ngang qua vị trí cân bằng)

$\Rightarrow T_{\min }=mg\left(\cos {\alpha }_0\right)$ (vật đạt vị trí biên)

3.5. Cơ năng, động năng, thế năng

● Khi bỏ qua ma sát, cơ năng của con lắc đơn được bảo toàn:

$\text{W}=\frac{1}{2}m{v}^2+mgl\left(1=\cos \alpha \right)=$ hằng số

● Động năng của con lắc đơn: $T=2\pi .\sqrt{\frac{l}{g}}$

● Thế năng của con lắc đơn tính ở ly độ góc: $W_t=mgl\left(1-\cos \alpha \right)$ (mốc tính thế năng ở vị trí cân bằng)

Từ 3 công thức cơ động năng và thế năng của con lắc đơn, ta có công thức tính năng lượng của con lắc đơn như sau: $\text{W}=W_d+{\text{W}}_t$

Trong đó:

W: Cơ năng của con lắc đơn

$W_d=\frac{1}{2}m{v}^2$ : Động năng của con lắc đơn(J)

${\text{W}}_{d\max }=\frac{1}{2}m{\omega }^2{S}^2=12m{v}_0^2$

${\text{W}}_t=m.g.h=mgl\left(1-\cos \alpha \right)$ : Thế năng của con lắc đơn(J)

$\Rightarrow {\text{W}}_{d\max }=mgl\left(1-\cos \alpha \right)$

Tương tự như con lắc lò xo, con lắc đơn có năng lượng luôn được bảo toàn.

$\text{W}=W_d+{\text{W}}_t=\frac{1}{2}m{v}^2+mgl\left(1-\cos \alpha \right)$ $={\text{W}}_{d\max }=\frac{1}{2}m{\omega }^2{S}^2=12m{v}_0^2$$=W_{t\max }=mgl\left(1-\cos \alpha \right)$

3.6. Lực kéo về

Lực kéo về (hay còn gọi là lực hồi phục) tác dụng lên con lắc đơn có độ lớn bằng:

$\left(F\right)=m\omega 2s=mg\alpha$ ( tính bằng rad)

4. Ứng dụng con lắc đơn

Trong thực tế đời sống, con lắc đơn có rất nhiều ứng dụng quan trọng, điển hình là dùng để xác định gia tốc rơi tự do trong lĩnh vực địa chất:

● Đo thời gian t của con lắc khi thực hiện n dao động toàn phần với công thức:

● Tính gia tốc trọng lượng của vật:

● Tính gia tốc rơi tự do tại một địa điểm khi tính giá trị trung bình ở nhiều lần đo

5. Ứng dụng: Xác định gia tốc rơi tự do

Trong lĩnh vực địa chất, các nhà địa chất quan tâm đến những tính chất đặc biệt của lớp bề mặt Trái Đất và thường xuyên phải đo gia tốc trọng trường ở một nơi nào đó. Sau đây là một ví dụ.

Dùng một con lắc có chiều dài l tính đến tâm của quả cầu. Đo thời gian của một số dao động toàn phần, từ đó suy ra chu kì T. Sau đó ta tính g theo công thức $g=\frac{4\pi 2.l}{T_2}$ . Lặp lại thí nghiệm nhiều lần, mỗi lần rút ngắn chiều dài con lắc đi một đoạn. Lấy giá trị trung bình g ở các lần đo, ta được gia tốc rơi tự do tại nơi đó.

6. Bài tập chu kì con lắc đơn

Câu 1: Một con lắc đơn có độ dài bằng l. Trong khoảng thời gian Δt nó thực hiện 12 dao động. Khi giảm độ dài của nó bớt 16cm, trong cùng khoảng thời gian Δt như trên, con lắc thực hiện 20 dao động. Cho biết $g=9,8m/s^2.$ Tính độ dài ban đầu của con lắc.

A. 40cm

B. 60cm

C. 50cm

D. 25cm

Lời giải:

Ta có: $T_1\frac{T_1}{T_2}=\sqrt{\frac{l_1}{l_2}}=\frac{N_2}{N_1}\iff \sqrt{\frac{l}{l-0,16}}=\frac{20}{12}\Rightarrow l=0,25m=25cm$

Chọn D

Câu 2: Một con lắc có độ dài $l_1$ dao động với chu kỳ $T_1=0,8s.$ Một con lắc đơn khác có độ dài $l_2$ dao động với chu kỳ $T_2=0,6s.$ Chu kỳ con lắc đơn có chiều dài $l_1+l_2$ là

A. 0,7s

B. 0,8s

C. 1s

D. 1,4s.

Lời giải:

Ta có: $T_{+}=\sqrt{T_1^2+T_2^2}=1s$

Câu 3: Một con lắc đơn có dây treo bằng kim loại, hệ số dãn nở của kim loại này là $1,{4.10}^{-5}$ độ ${-1}^{}$ , con lắc đơn dao động tại một điểm cố định trên mặt đất, có chu kỳ 2s lúc ở ${10}^{o}C.$ Nếu tăng nhiệt độ thêm ${20}^{o}C$ thì chu kỳ sẽ

A. tăng $2,{8.10}^{-4}.$

B. giảm $2,{8.10}^{-4}.$

C. tăng $4,{2.10}^{-4}.$

D. giảm $4,{2.10}^{-4}.$

Lời giải:

Ta có: $T_2=\frac{T_1}{1-\frac{1}{2}\lambda \left(t_2-t_1\right)}=T_1\left(1+\frac{1}{2}\lambda \left(t_2-t_1\right)\right)=2,00028s\Rightarrow$ T tăng $2,{8.10}^{-4}s$

Câu 4: Tại cùng một địa điểm thực hiện thí nghiệm với con lắc đơn có chiều dài $l_1$ thì dao động với chu kỳ $T_1,$ con lắc đơn $l_2$ thì dao động với chu kỳ $T_2$.Hỏi nếu thực hiện thực hiện thí nghiệm với con lắc đơn có chiều dài $l=l_1+l_2$ thì con lắc đơn dao động với chu kỳ T là bao nhiêu?

A. $T=T_1^2.T_2^2$

B. $T^2=\frac{T_1^2.T_2^2}{\sqrt{T_1^2+T_2^2}}$

C. $T^2=T_1^2+T_2^2$

D. $T=T_1^{-2}+T_2^{-2}$

Lời giải:

Chọn C

Gọi $T_1$ là chu kỳ của con lắc có chiều dài $l_1$

$\Rightarrow T_1=2\pi \sqrt{\frac{l_1}{g}}\Rightarrow T_1^2=4{\pi }^2\frac{l_1}{g}$

Gọi $T_2$ là chu kỳ của con lắc có chiều dài $l_2$

$\Rightarrow T_2=2\pi \sqrt{\frac{l_2}{g}}\Rightarrow T_2^2=4{\pi }^2\frac{l_2}{g}$

T là chu kỳ của con lắc có chiều dài $l=l_1+l_2$

$\Rightarrow T=2\pi \sqrt{\frac{l}{g}}=2\pi \sqrt{\frac{l_1+l_2}{g}}$

$\Rightarrow T^2=4{\pi }^2\frac{l_1+l_2}{g}=4{\pi }^2\frac{l_1}{g}+4{\pi }^2\frac{l_2}{g}$

$=T_1^2+T_2^2$

Câu 5: Một con lắc đơn được treo vào trần một thang máy. Khi thang máy chuyển động thẳng đứng đi lên nhanh dần đều với gia tốc có độ lớn a thì chu kì dao động điều hòa của con lắc là 2,52 s. Khi thang máy chuyển động thẳng đứng đi lên chậm dần đều với gia tốc cũng có độ lớn a thì chu kì dao động điều hòa của con lắc là 3,15 s. Khi thang máy đứng yên thì chu kì dao động điều hòa của con lắc là

A. 2,96 s

B. 2,84 s

C. 2,61 s

D. 2,78 s

Lời giải:

Chọn D

$\frac{T_1}{T_2}=\sqrt{\frac{g-a}{g+a}}\to T_2^2\left(g-a\right)=T_1^2\left(g+a\right)$

$\to a=\frac{\left(T_2^2-T_1^2\right)g}{T_1^2+T_2^2}=0,22g$

$\frac{T}{T_1}=\sqrt{\frac{g+a}{g}}=\sqrt{1,22}\to T=T_1.\sqrt{1,22}=2,78s$

Xem thêm các bài viết để học tốt môn Vật Lí sách mới hay, chi tiết khác:

• Tụ điện là gì? Công thức tính tụ điện

• Chuyển động cơ học là gì? Công thức tính chuyển động cơ học

• Chuyển động nhanh dần đều là gì? Công thức tính chuyển động nhanh dần đều

• Cơ năng là gì? Công thức tính cơ năng

• Vật nhiễm điện là gì? Công thức tính vật nhiễm điện

• Con lắc lò xo là gì? Công thức tính con lắc lò xo

---