Bài toán thực tế lớp 10 Vectơ

Bài toán thực tế lớp 10 Vectơ có lời giải chương trình mới dùng chung cho ba sách Kết nối tri thức, Chân trời sáng tạo, Cánh diều với bài tập đa dạng giúp Giáo viên có thêm tài liệu giảng dạy các dạng toán thực tế lớp 10.

Bài toán thực tế lớp 10 Vectơ

Xem thử

Chỉ từ 300k mua trọn bộ Chuyên đề, các dạng Toán thực tế lớp 10 chương trình mới bản word trình bày đẹp mắt, chỉnh sửa dễ dàng:

• B1: gửi phí vào tk: 1053587071 - NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

A. KIẾN THỨC CẦN NHỚ

I. KHÁI NIỆM VECTO

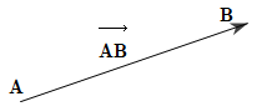
1. Cho đoạn thẳng AB. Nếu ta chọn điềm A làm điêm đầu, điểm B làm điểm cuối thì ta được đoạn thẳng AB có hướng từ A đến B. Đoạn thẳng có định hướng AB được kí hiệu là $\overrightarrow{AB}$ và được gọi là vectơ $\overrightarrow{AB}$.

2.

- Vectơ có điểm đầu A, điểm cuốiB được kí hiệu là $\overrightarrow{AB}$, đọc là vectơ $\overrightarrow{AB}$

- Đường thẳng đi qua hai điểm A và B gọi là giá của vectơ $\overrightarrow{AB}$.

- Độ dài của đoạn thẳng AB gọi là độ dài của vectơ $\overrightarrow{AB}$ và được kí hiệu là $\left|\overrightarrow{AB}\right|$. Như vậy ta có: $\left|\overrightarrow{AB}\right|=AB$

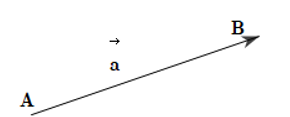
3. Một vectơ khi không cần chỉ rõ điểm đầu và điểm cuối có thể viết là $\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y},\dots$

4. Vectơ có độ dài bằng 1 gọi là vectơ đơn vị.

5. Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

6. Nếu hai vectơ cùng phương thì chúng chỉ có thể cùng hướng hoặc ngược hướng.

7. Ba điểm phân biệt A, B, C thẳng hàng khi và chi khi hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương.

8. Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu $\overrightarrow{a}=\overrightarrow{b}$.

9. Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài, kí hiệu $\overrightarrow{a}=-\overrightarrow{b}$. Khi đó, vectơ $\overrightarrow{b}$ được gọi là vectơ đối của vectơ $\overrightarrow{a}$.

10. Cho vectơ $\overrightarrow{a}$ và điểm O, ta luôn tìm được một điểm A duy nhất sao cho: $\overrightarrow{OA}=\overrightarrow{a}$

11. Với một điểm A bất kì, ta quy ước có một vectơ đặc biệt mà điểm đầu và điểm cuối đều là A. Vectơ này được kí hiệu là $\overrightarrow{AA}$ và gọi là vecto-không. Ta kí hiệu vecto-không là $\overrightarrow{0}$. Như vậy $\overrightarrow{0}=\overrightarrow{AA}=\overrightarrow{BB}=\overrightarrow{CC}=\dots$ với mọi điểm $A,B,C,\dots .$

12. Vectơ-không có độ dài bằng 0 và cùng hướng với mọi vectơ.

II. CỘNG, TRỪ HAI VECTƠ

1. Quy tắc ba điểm

Với ba điểm A, B , C, ta có: $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.

2. Quy tắc hình bình hành

Nếu OABC là hình bình hành thì ta có $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}\text{. }$

3. Tính chất của phép cộng các vectơ

- Tính chất giao hoán: $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}$;

- Tính chất kết hợp: $(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})$;

- Với mọi vectơ $\overrightarrow{a}$, ta luôn có: $\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a}$.

4. Hiệu của hai vectơ

Cho hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$. Hiệu của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ là vectơ $\overrightarrow{a}+(-\overrightarrow{b})$ và kí hiệu $\overrightarrow{a}-\overrightarrow{b}$

Chú ý: Cho ba điểm O, A, B như Hình 4, ta có $\overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{AB}$.

5. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác

Điểm M là trung điểm của đoạn thẳng AB khi và chỉ khi $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$.

Điểm G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

III. TÍCH CỦA MỘT VECTƠ VỚI MỘT SỐ

1. Tích của một số với một vectơ và các tính chất

- Cho số k khác 0 và vectơ $\overrightarrow{a}$ khác $\overrightarrow{0}$. Tích của số k với vectơ $\overrightarrow{a}$ là một vectơ, kí hiệu là $k\overrightarrow{a}$.

Vectơ $k\overrightarrow{a}$ cùng hướng với $\overrightarrow{a}$ nếu k > 0, ngược hướng với $\overrightarrow{a}$ nếu k < 0 và có độ dài bằng $\left|k\right|.\left|\overrightarrow{a}\right|$.

Quy ước: $0\overrightarrow{a}=\overrightarrow{0}$ và $k\overrightarrow{0}=\overrightarrow{0}$.

- Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bất kì, với mọi số thực h và k, ta có:

- $•k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{a}+k\overrightarrow{b};$

$•(h+k)\overrightarrow{a}=h\overrightarrow{a}+k\overrightarrow{a};$

$•h(k\overrightarrow{a})=(hk)\overrightarrow{a};$

- $•1.\overrightarrow{a}=\overrightarrow{a};$$•(-1)\cdot \overrightarrow{a}=-\overrightarrow{a}$

2. Điều kiện để hai vectơ cùng phương

Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}(\overrightarrow{b}$ khác $\overrightarrow{0})$ cùng phương khi và chi khi có một số k sao cho $\overrightarrow{a}=k\overrightarrow{b}$.

3. Điều kiện để ba điểm thẳng hàng

Ba điểm phân biệt A, B , C thẳng hàng khi và chỉ khi có số k khác 0 để $\overrightarrow{AB}=k\overrightarrow{AC}$.

IV. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ

1. Góc giữa hai vectơ

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác $\overrightarrow{0}$. Từ một điểm O bất kì ta vẽ $\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$.

Góc $\widehat{AOB}$ với số đo từ $0^{°}$ đến ${180}^{°}$ được gọi là góc giữa hai vectơ  $\overrightarrow{a}$ và $\overrightarrow{b}$.

Ta kí hiệu góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ là $(\overrightarrow{a},\overrightarrow{b})$

Nếu $(\overrightarrow{a},\overrightarrow{b})={90}^{°}$ thì ta nói rằng $\overrightarrow{a}$ và $\overrightarrow{b}$ vuông góc với nhau, kí hiệu là $\overrightarrow{a}\perp \overrightarrow{b}$.

Chú ý:

- Từ định nghĩa ta có $(\overrightarrow{a},\overrightarrow{b})=(\overrightarrow{b},\overrightarrow{a})$.

- Góc giữa hai vectơ cùng hướng và khác $\overrightarrow{0}$ luôn bằng 0.

- Góc giữa hai vectơ ngược hướng và khác $\overrightarrow{0}$ luôn bằng ${180}^{°}$.

- Trong trường hợp có ít nhất một trong hai vectơ $\overrightarrow{a}$ hoặc $\overrightarrow{b}$ là vectơ $\overrightarrow{0}$ thì ta quy ước số đo góc giữa hai vectơ đó là tuỳ ý (từ 0° đến ${180}^{°}$).

2. Tích vô hướng của hai vectơ

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác $\overrightarrow{0}$.

Tích vô hướng của $\overrightarrow{a}$ và $\overrightarrow{b}$ là một số, kí hiệu là $\overrightarrow{a}.\overrightarrow{b}$, được xác định bởi công thức: $\overrightarrow{a}\cdot \overrightarrow{b}=\left|\overrightarrow{a}\right|\cdot \left|\overrightarrow{b}\right|\cdot \cos (\overrightarrow{a},\overrightarrow{b})$

Chú ý:

- Trường hợp ít nhất một trong hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bằng $\overrightarrow{0}$, ta quy ước $\overrightarrow{a}\cdot \overrightarrow{b}=0$.

- Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác $\overrightarrow{0}$, ta có $\overrightarrow{a}\perp \overrightarrow{b}\iff \overrightarrow{a}\cdot \overrightarrow{b}=0$.

-Khi $\overrightarrow{a}=\overrightarrow{b}$ thì tích vô hướng $\overrightarrow{a}\cdot \overrightarrow{b}$ được kí hiệu là ${\overrightarrow{a}}^2$ và được gọi là bình phương vô hướng của vectơ $\overrightarrow{a}$.

Ta có ${\overrightarrow{a}}^2=\left|\overrightarrow{a}\right|\cdot \left|\overrightarrow{a}\right|\cdot \cos 0^{°}=|\overrightarrow{a}{|}^2$. Vậy bình phương vô hướng của một vectơ luôn bằng bình phương độ dài của vectơ đó.

3. Tính chất của tích vô hướng

- Với ba vectơ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ bất kì và mọi số k, ta có:

$•\overrightarrow{a}\cdot \overrightarrow{b}=\overrightarrow{b}\cdot \overrightarrow{a};$

$•\overrightarrow{a}\cdot (\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}\cdot \overrightarrow{b}+\overrightarrow{a}\cdot \overrightarrow{c};$

$•(k\overrightarrow{a})\cdot \overrightarrow{b}=k(\overrightarrow{a}\cdot \overrightarrow{b})=\overrightarrow{a}\cdot (k\overrightarrow{b})$

- Từ các tính chất của tích vô hướng của hai vectơ, ta suy ra:

- $•{(\overrightarrow{a}+\overrightarrow{b})}^2={\overrightarrow{a}}^2+2\overrightarrow{a}\cdot \overrightarrow{b}+{\overrightarrow{b}}^2;$

$•{(\overrightarrow{a}-\overrightarrow{b})}^2={\overrightarrow{a}}^2-2\overrightarrow{a}\cdot \overrightarrow{b}+{\overrightarrow{b}}^2$

- $•(\overrightarrow{a}+\overrightarrow{b})\cdot (\overrightarrow{a}-\overrightarrow{b})={\overrightarrow{a}}^2-{\overrightarrow{b}}^2$

4. Áp dụng của tích vô hướng

Trong Vật lí, tích vô hướng giúp tính công A sinh bởi một lực $\overrightarrow{F}$ có độ dịch chuyển là vectơ $\overrightarrow{d}$. Ta có công thức: $A=\overrightarrow{F}\cdot \overrightarrow{d}$.

B. BÀI TẬP VẬN DỤNG

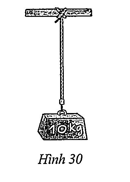
Câu 1: Treo một vật có khối lượng 10kg vào một sợi dây (Hình 30). Sử dụng vectơ $\overrightarrow{P}$ để biểu diễn trọng lực, vectơ $\overrightarrow{T}$ để biểu diễn lực căng của dây tác dụng lên vật đó. Chọn các khẳng định đúng trong các phát biểu sau:

a) $\overrightarrow{P}$ có phương thẳng đứng;

b) $\overrightarrow{T}$ có phương thẳng đứng;

c) $\overrightarrow{P}$ có hướng từ trên xuống dưới;

d) $\overrightarrow{P}$ có hướng từ dưới lên trên;

e) $\overrightarrow{T}$ có hướng từ trên xuống dưới;

g) $\overrightarrow{T}$ có hướng từ dưới lên trên.

Giải

Các phát biểu đúng là a, b, c, g.

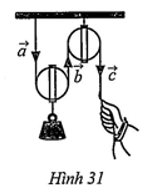
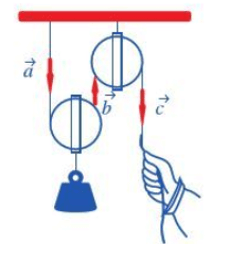
Câu 2: Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ (Hình 31 ).

a) Hãy chỉ ra các cặp vectơ cùng phương.

b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng?

Giải

a) Các cặp vectơ cùng phương là $\overrightarrow{a}$ và $\overrightarrow{b},\overrightarrow{b}$ và $\overrightarrow{c},\overrightarrow{c}$ và $\overrightarrow{a}$.

b) Cặp vectơ cùng hướng là $\overrightarrow{c}$ và $\overrightarrow{a}$. Các cặp vectơ ngược hướng là $\overrightarrow{a}$ và $\overrightarrow{b},\overrightarrow{b}$ và $\overrightarrow{c}$.

Câu 3: Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectoo $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$(hình)

a) Hãy chỉ ra các cặp vectơ cùng phương.

b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.

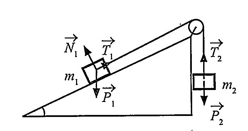
Câu 4: Trong mặt phẳng nghiêng không có ma sát, cho hệ vật $m_1,m_2$, hai vật nối với nhau bằng một sợi dây không dãn vắt qua ròng rọc (Hình 32). Giả sử bỏ qua khối lượng của dây và ma sát của ròng rọc.

a) Tìm các cặp vectơ cùng phương trong các vectơ ở Hinh 32.

b) Những cặp vectơ cùng phương đó có cùng hướng không?

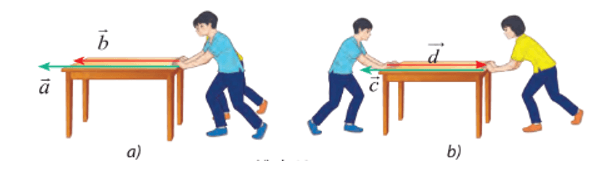
Câu 5: Tìm các lực cùng hướng và ngược hướng trong số các lực đẩy được biểu diễn bằng các vectơ trong hình

Câu 6: Trên biển Đông, một tàu chuyển động đều từ vị trí A theo hướng $N{20}^{°}E$ với vận tốc 20km/h. Sau 2 giờ, tàu đến được vị trí B. Hỏi A cách B bao nhiêu kilômét và về hướng nào so với B?

Câu 7: Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc là 10km/h. Một chiếc ca nô chuyển động từ phía đông sang phía tây với vận tốc 40km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông.

................................

................................

................................

Xem thử

Xem thêm Chuyên đề Toán thực tế lớp 10 chương trình mới có lời giải hay khác:

• Bài toán thực tế lớp 10 Hệ thức lượng trong tam giác

• Bài toán thực tế lớp 10 Hàm số bậc hai

• Bài toán thực tế lớp 10 Hai phương trình quy về phương trình bậc hai

• Bài toán thực tế lớp 10 Các số đặc trưng đo xu thế trung tâm

• Bài toán thực tế lớp 10 Đường thẳng

• Bài toán thực tế lớp 10 Phương trình đường tròn

---