Bài toán thực tế lớp 10 Đường thẳng

Bài toán thực tế lớp 10 Đường thẳng có lời giải chương trình mới dùng chung cho ba sách Kết nối tri thức, Chân trời sáng tạo, Cánh diều với bài tập đa dạng giúp Giáo viên có thêm tài liệu giảng dạy các dạng toán thực tế lớp 10.

Bài toán thực tế lớp 10 Đường thẳng

Xem thử

Chỉ từ 300k mua trọn bộ Chuyên đề, các dạng Toán thực tế lớp 10 chương trình mới bản word trình bày đẹp mắt, chỉnh sửa dễ dàng:

• B1: gửi phí vào tk: 1053587071 - NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

A. KIẾN THỨC CƠ BẢN CẦN NẮM

1. Phương trình tham số của đường thẳng

- Vectơ $\overrightarrow{u}$ được gọi là vectơ chỉ phưong của đường thẳng $\Delta$ nếu $\overrightarrow{u}\ne \overrightarrow{0}$ và giá của $\overrightarrow{u}$ song song hoặc trùng với $\Delta$.

- Hệ $\left\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\end{array}\left(a^2+b^2>0\right.\right.$ và t là tham số) được gọi là phưong trình tham số của đường thẳng $\Delta$ đi qua $M_0\left(x_0;y_0\right)$ và nhận $\overrightarrow{u}=(a;b)$ làm vectơ chỉ phương.

2. Phương trình tổng quát của đường thẳng

- Vectơ $\overrightarrow{n}$ được gọi là vectơ pháp tuyến của đường thẳng $\Delta$ nếu $\overrightarrow{n}\ne \overrightarrow{0}$ và giá của $\overrightarrow{n}$ vuông góc với $\Delta$.

Nhận xét: Nếu đường thẳng $\Delta$ có vectơ chỉ phương là $\overrightarrow{u}=(a;b)$ thì vectơ $\overrightarrow{n}=(-b;a)$ là một vectơ pháp tuyến của $\Delta$ và ngược lại.

- Phương trình ax + by + c = 0 ( a và b không đồng thời bằng 0 ) được gọi là phương trình tổng quát của đường thẳng.

3. Lập phương trình đường thẳng

a) Lập phương trình đường thẳng đi qua một điểm và biết vectơ pháp tuyến Phương trình đường thẳng $\Delta$ đi qua điểm $M_0\left(x_0;y_0\right)$ và nhận $\overrightarrow{n}=(a;b)(\overrightarrow{n}\ne \overrightarrow{0})$ làm vectơ pháp tuyến là $a\left(x-x_0\right)+b\left(y-y_0\right)=0$.

b) Lập phương trình đường thẳng đi qua một điểm và biết vectơ chỉ phương

Phương trình tham số của đường thẳng $\Delta$ đi qua điểm $M_0\left(x_0;y_0\right)$ và nhận $\overrightarrow{u}=(a;b)(\overrightarrow{u}\ne \overrightarrow{0})$ làm vectơ chỉ phương là: $\left\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\end{array}\right.$(t là tham số)

Nếu $a\ne 0$ và $b\ne 0$ thì ta còn có thể viết phương trình của đường thẳng $\Delta$ ở dạng:

$\frac{x-x_0}{a}=\frac{y-y_0}{b}\text{. }$

c) Lập phương trình đường thẳng đi qua hai điểm

Phương trình tham số của đường thẳng $\Delta$ đi qua hai điểm $A\left(x_0;y_0\right),B\left(x_1;y_1\right)$ là:

$\left\{\begin{array}{l}x=x_0+\left(x_1-x_0\right)t\\ y=y_0+\left(y_1-y_0\right)t\end{array}\right.$(t là tham số)

Nếu $x_1-x_0\ne 0$ và $y_1-y_0\ne 0$ thì ta còn có thể viết phương trình của đường thẳng $\Delta$ ở dạng: $\frac{x-x_0}{x_1-x_0}=\frac{y-y_0}{y_1-y_0}$.

Chú ý: Đường thẳng $\Delta$ đi qua hai điểm A(a; 0) và $B(0;b)(ab\ne 0)$ có phương trình $\frac{x}{a}+\frac{y}{b}=1$, gọi là phương trình đường thẳng theo đoạn chắn.

4. Vị trí tương đối của hai đường thẳng

a) Trong mặt phẳng toạ độ, cho hai đường thẳng ${\Delta }_1,{\Delta }_2$ lần lượt có vectơ chỉ phương là ${\overrightarrow{u}}_1,{\overrightarrow{u}}_2$. Khi đó

- ${\Delta }_1$ cắt ${\Delta }_2$ khi và chỉ khi ${\overrightarrow{u}}_1,{\overrightarrow{u}}_2$ không cùng phương.

- ${\Delta }_1$ song song với ${\Delta }_2$ khi và chỉ khi ${\overrightarrow{u}}_1,{\overrightarrow{u}}_2$ cùng phương và có một điểm thuộc một đường thẳng mà không thuộc đường thẳng còn lại.

- ${\Delta }_1$ trùng với ${\Delta }_2$ khi và chỉ khi ${\overrightarrow{u}}_1,{\overrightarrow{u}}_2$ cùng phương và có một điểm thuộc cả hai đường thẳng đó.

Chú ý: ${\Delta }_1$ vuông góc với ${\Delta }_2$ khi và chỉ khi ${\overrightarrow{u}}_1,{\overrightarrow{u}}_2$ vuông góc với nhau.

b) Cho hai đường thẳng ${\Delta }_1$ và ${\Delta }_2$ có phương trình lần lượt là: $a_{1}x+b_{1}y+c_1=0;a_{2}x+b_{2}y+c_2=0.$

Xét hệ phương trình: $\left\{\begin{array}{l}{a}_{1}x+b_{1}y+c_1=0\\ a_{2}x+b_{2}y+c_2=0\end{array}\right.$

Khi đó

- ${\Delta }_1$ song song với ${\Delta }_2$ khi và chỉ khi hệ (I) vô nghiệm.

- ${\Delta }_1$ trùng với ${\Delta }_2$ khi và chỉ khi hệ (I) có vô số nghiệm.

5. Góc giữa hai đường thẳng

Trong mặt phẳng toạ độ, cho hai đường thẳng ${\Delta }_1$ và ${\Delta }_2$ có vectơ chỉ phương lần lượt là ${\overrightarrow{u}}_1=\left(a_1;b_1\right),{\overrightarrow{u}}_2=\left(a_2;b_2\right)$. Khi đó $\cos \left({\Delta }_1,{\Delta }_2\right)=\frac{\left|a_1{a}_2+b_1{b}_2\right|}{\sqrt{a_1^2+b_1^2}\cdot \sqrt{a_2^2+b_2^2}}$

Nhận xét

- ${\Delta }_1\perp {\Delta }_2\iff a_1{a}_2+b_1{b}_2=0$.

- Cho hai đường thẳng ${\Delta }_1$ và ${\Delta }_2$ có vectơ pháp tuyến lần lượt là ${\overrightarrow{n}}_1,{\overrightarrow{n}}_2$. Ta cũng có: $\cos \left({\Delta }_1,{\Delta }_2\right)=\left|\cos \left({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\right)\right|=\frac{\left|{\overrightarrow{n}}_1\cdot {\overrightarrow{n}}_2\right|}{\left|{\overrightarrow{n}}_1\right|\cdot \left|{\overrightarrow{n}}_2\right|}.$

6. Khoảng cách từ một điểm đến một đường thẳng

Trong mặt phẳng toạ độ Oxy, cho đường thẳng $\Delta$ có phương trình $ax+by+c=0$ $\left(a^2+b^2>0\right)$ và điểm $M\left(x_0;y_0\right)$. Khoảng cách từ điểm Mđến đường thẳng $\Delta$, kí hiệu là $d(M,\Delta )$, được tính bởi công thức sau: $d(M,\Delta )=\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$

Chú ý: Nếu $M\in \Delta$ thì $d(M,\Delta )=0$.

B. BÀI TẬP VẬN DỤNG

Câu 1: Để tham gia một phòng tập thể dục, người tập phải trả một khoản phí tham gia ban đầu và phí sử dụng phòng tập. Đường thẳng $\Delta$ ở Hình 38 biểu thị tổng chi phí (đơn vị: triệu đồng) để tham gia một phòng thập thể dục theo thời gian tập của một người (đơn vị: tháng).

a. Viết phương trình của đường thẳng $\Delta$.

b. Giao điểm của đường thẳng $\Delta$ với trục tung trong tình huống này có ý nghĩa gì?

c. Tính tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng.

Lời giải

a. $\Delta$ qua A(7; 5) và B(0; 1; 5), nhận $\overrightarrow{AB}(-7;-3,5)$ làm vecto chỉ phương có phương trình là:

$\Delta :\left\{\begin{array}{l}x=7-7t\\ y=5-3,5t\end{array}\right.$ (t là tham số).

b. Giao điểm của đường thẳng $\Delta$ với trục tung trong tình huống này có ý nghĩa là: khoản phí tham gia ban đầu mà người tập phải trả.

c. Tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng là:

x = 12 thay vào phương trình của $\Delta$ ta được: $\left\{\begin{array}{l}12=7-7t\\ y=5-3,5t\end{array}\right.$

$\iff \left\{\begin{array}{l}12=7-7t\\ y=5-3,5t\end{array}\right.$$\iff \left\{\begin{array}{l}t=\frac{-5}{7}\\ y=5-3,5\cdot \left(\frac{-5}{7}\right)\end{array}\right.$$\iff \left\{\begin{array}{l}t=\frac{-5}{7}\\ y=7,5\end{array}\right.$

Vậy Tổng chi phí mà người đo phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng là: 7,5 triệu đồng.

Câu 2: Theo Google Maps, sân bay Nội Bài có vĩ độ $21,2°$ Bắc, kinh độ 105,8° Đông, sân bay Đà Nẵng có vĩ độ 16,1° Bắc, kinh độ 108,2° Đông. Một máy bay, bay từ Nội Bài đến sân bay Đà Nẵng. Tại thời điểm t giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ $x^0$ Bắc, kinh độ $y^0$ Đông được tính theo công thức

$\left\{\begin{array}{l}x=21,2-\frac{153}{40}t\\ y=105,8+\frac{9}{5}t\end{array}\right.$

a. Hỏi chuyến bay từ Hà Nội đến Đà Nẵng mất mấy giờ?

b. Tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ̃ tuyến 17 ( $\left.{17}^{0}B?c\right)$ chưa?

Lời giải

a. Nếu máy bay đến Đà Nã̃ng thì x = 16,1 và y = 108,2

Ta có: $\left\{\begin{array}{l}16,1=21,2-\frac{153}{40}t\\ 108,2=105,8+\frac{9}{5}t\end{array}\right.$ $\iff t=\frac{4}{3}$

Vậy chuyến bay từ Hà Nội đến Đà Nã̃ng mất gần 1,33 giờ

b. Tại thời điểm 1 giờ thì t  = 1 thay vào phương trình có:

$\left\{\begin{array}{c}x=21,2-\frac{153}{40}.1=17,375\\ y=105,8+\frac{9}{5}.1=107,6\end{array}\right.$

Vậy tại thời điểm 1 giờ, máy bay đã qua vĩ tuyến 17 .

Câu 3: Một người đang viết chương trình cho trò chơi bóng đá rô bốt. Gọi $A(-1;1),B(9;6),C(5;-3)$ là ba vị trí trên màn hình.

a. Viết phương trình các đường thẳng $AB,AC,BC$.

b. Tính góc hợp bởi hai đường thẳng AB và AC.

c. Tính khoảng cách từ điểm A đến đường thẳng BC.

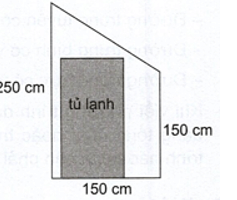
Câu 4: Nhà bạn Nam định đổi tủ lạnh và dự định kê vào vị trí dưới cầu thang. Biết vị trí định kê tủ lạnh có mặt cắt là một hình thang vuông với hai đáy lần lượt là 150cm và 250cm, chiều cao là 150 cm (như hình vẽ). Bố mẹ bạn Nam định mua một 250cm tủ lạnh 2 cánh (Side by side) có chiều cao là 183 cm và bề ngang 90cm. Bằng cách sử dụng toạ độ trong mặt phẳng, em hãy giúp Nam tính xem bố mẹ bạn Nam có thể kê vừa chiếc tủ lạnh vào vị trí cần kê không?

Câu 5: Một trạm viễn thông S có toạ độ (5;1). Một người đang ngồi trên chiếc xe khách chạy trên đoạn cao tốc có dạng một đường thẳng $\Delta$ có phương trình $12x+5y-20=0$. Tính khoảng cách ngắn nhất giữa người đó và trạm viễn thông S. Biết rằng mỗi đơn vị độ dài tương ứng với 1km.

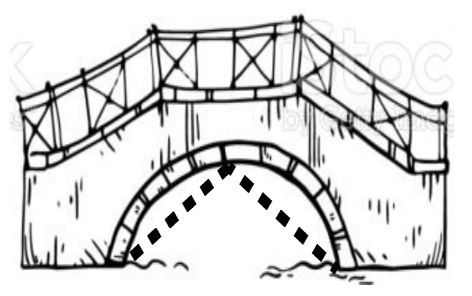
Câu 6: Trong giai đoạn sửa chữa cầu, nhà thầu thi công gia cố thêm hệ thống chịu tải là 2 thanh sắt có độ dài bằng nhau (được vẽ nét đứng trong hình).

Biết phần cong của cây cầu là nửa đường cong bán kính là 2 mét. Xác định phương trình đường thẳng của những thanh chịu tải.

Câu 7: Trong mặt phẳng tọa độ, một thiết bị âm thanh được phát từ vị trí A(4; 4). Người ta dự định đặt một máy thu tín hiệu trên đường thẳng có phương trình $x-y-3=0$. Hỏi máy thu đặt ở vị trí nào sẽ nhận được tín hiệu sớm nhất.

................................

................................

................................

Xem thử

Xem thêm Chuyên đề Toán thực tế lớp 10 chương trình mới có lời giải hay khác:

• Bài toán thực tế lớp 10 Hai phương trình quy về phương trình bậc hai

• Bài toán thực tế lớp 10 Các số đặc trưng đo xu thế trung tâm

• Bài toán thực tế lớp 10 Phương trình đường tròn

• Bài toán thực tế lớp 10 Ba đường Conic

• Bài toán thực tế lớp 10 Đại số tổ hợp

• Bài toán thực tế lớp 10 Xác suất

---